【資格の勉強】浮動小数点形式

浮動小数点形式とは、符号部、指数部、仮数部の3つのパーツで小数点数を表す。

符号部は、1ビットで正の数か負の数かを表す部分のこと。0は正、1は負を表す。浮動小数点においては、小数点以上（一番左）にある1桁を指す。

指数部は、累乗を表す部分のこと。2³の場合、3乗の「3」を2進数で表す「11」となる。

仮数部は、値の本体部分のこと。浮動小数点形式においては、小数点以下の部分を指す。

符号部、指数部、仮数部の順番に書く。また、指定されたビットより値が少なければ、指数部は右詰め、仮数部は左詰めでそれぞれ書くというルールがある。空欄は0で埋める。

浮動小数点形式に関する、基本情報技術者試験の過去問は以下を参照。

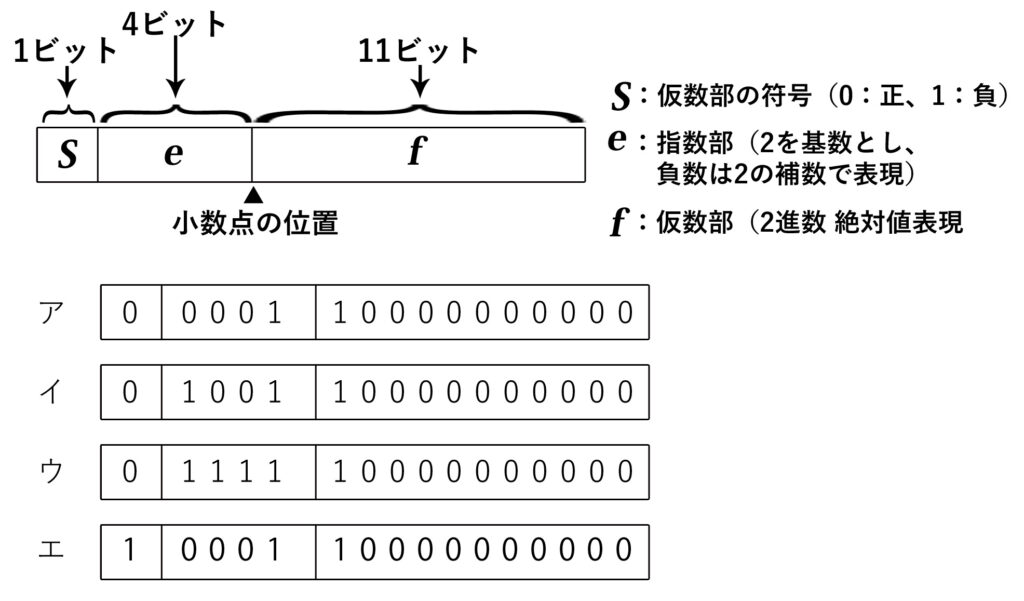
数値を図に示す16ビットの浮動小数点形式で表すとき、10進数0.25を正規化した表現はどれか。ここでの正規化は、仮数部の最上位けたが0にならないように指数部と仮数部を調節する操作とする。

まず、10進数「0.25」を2進数にすると「0.01」になる。

正規化の条件として「仮数部の最上位桁が0にならないようにする」とあるので、仮数部の最上位桁は「1」が確定している。仮数部は小数点以下で表すので「0.01」は「0.1」に変換される。

更に仮数部は11ビットという指定があるため「10000000000」となるのだが、すべての選択肢で同じ値になっているので、答えの成否は判断はできない。

次に指数部。上記の正規化条件により「0.1」を作る必要がある。「0.1」を使って「0.01」を表すには、「0.1×2^-1（＝0.01）」という式が成立する。指数部の「-1」を4ビットの2進数、なおかつマイナスなので2の補数表現で表さなければならない。

つまり、「1」を2進数の「0001」とし、反転して「1110」にし、1を加えて「1111」とする。

最後に、仮数部は正の数なので、符号ビットで正を表す「0」を加える。

これらを、符号、指数部、仮数部の順番に並べると「0 1111 10000000000」となる。正解は「ウ」。